EFFICIENT MODULE TRANSFERS AND MOVEMENTS

When there is a need for a module at a particular location in a matrix where there currently isn’t one, there is more that one way to get a module to that location. Figure 5a shows a matrix of modules. The top row has a module A at the left end on the diagram. The bottom row has an arbitrary sized series of modules connected together, including modules B, C, and D, along with some unlabeled modules. A module at the right end of the matrix on top of the bottom row is desired, so that there is a pattern arrangment that consists of having a module mounted on top of the module that happens to be labeled D. The labels identifying these modules are only abstract labels, for showing where the modules physically move to when they move around.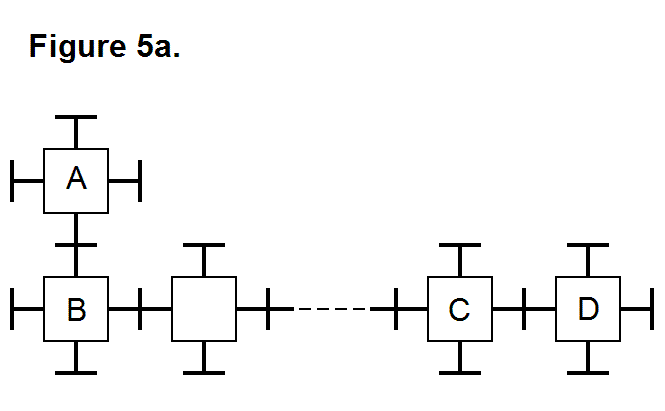

One techique of accomplishing this is to take module A and transfer it along the top of the bottom row matrix modules so that the matrix will have a module present at the desired location. Figure 5b shows the matrix with module A moved to the location where a module is desired in the matrix.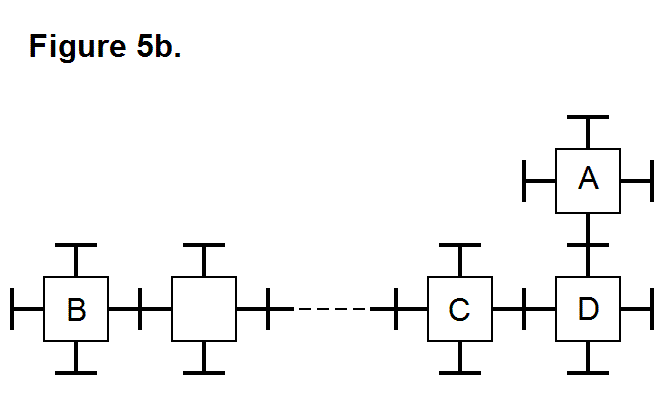

If the bottom row of modules is significantly long, there’s a faster and simpler way of getting the same pattern without the need of transferring module A from the left end of the top of the matrix all the way to the right end. This is achieved by placing module D on top of module C to get the matrix arranged in the desired pattern. This is simpler and quicker because it can be done in one move using a different module, instead of several moves based on the number of modules in the bottom row using module A. Figure 5c shows the matrix pattern when this technique is used. In this version, module A can be moved down to the left end of the bottom row if a specific pattern is required on this side.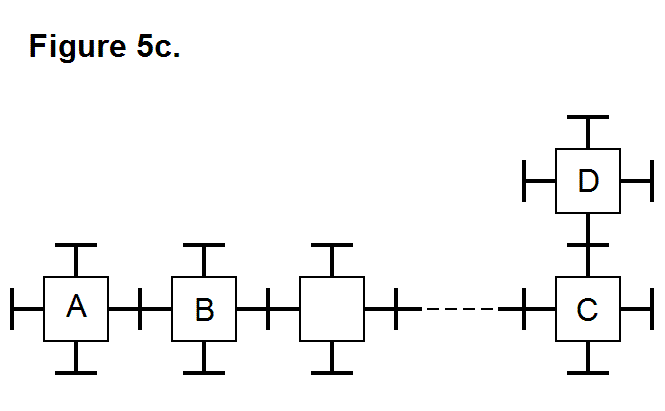

This technique is beneficial for replacing failed or missing modules, or reshaping a matrix of modules, by significantly reducing the amount of time and energy that would have been consumed if this technique was not utilized. A matrix of modules can easily change from one shape or application to another one that is completely different with a minimal amount of effort by utilizing this technique for every module that needs to be moved into a position in the matrix.