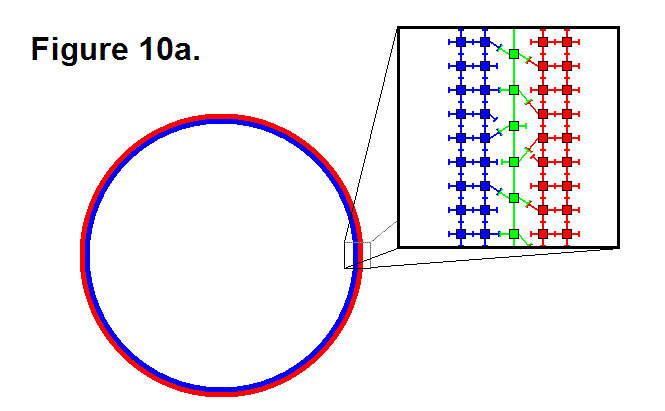
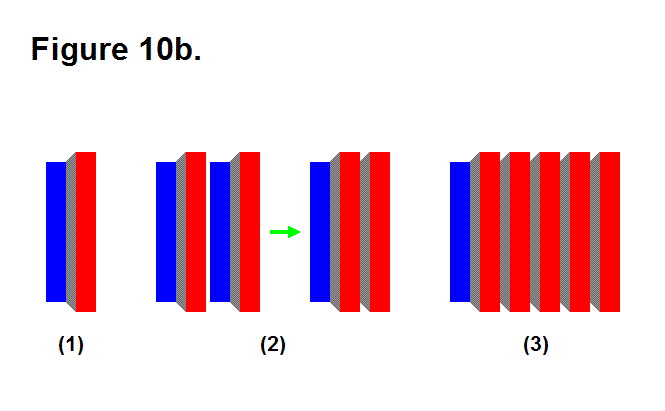
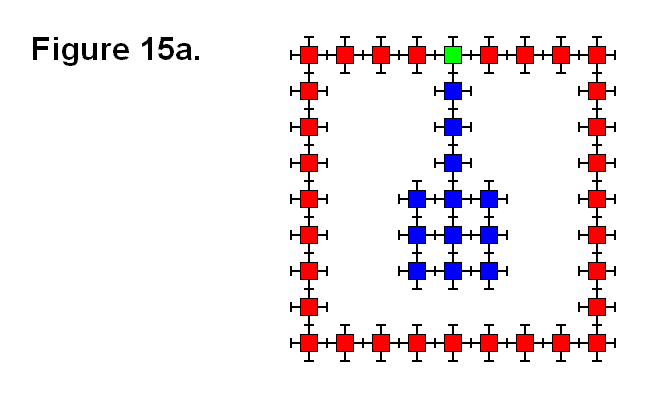
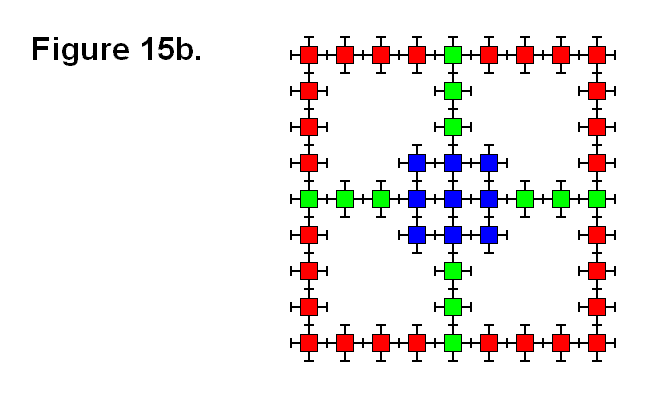
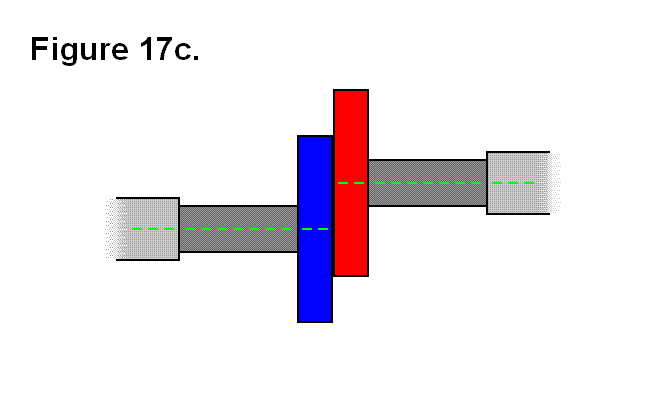
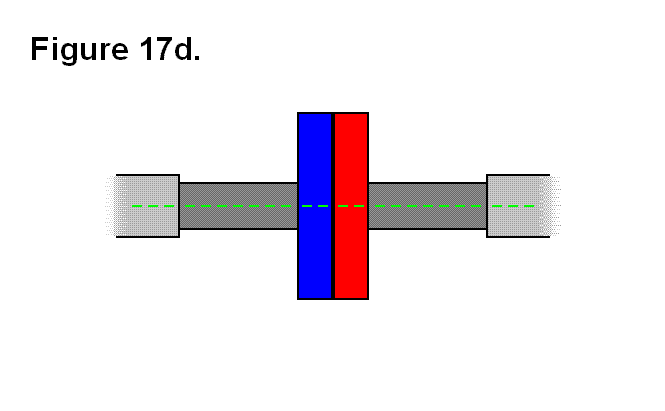
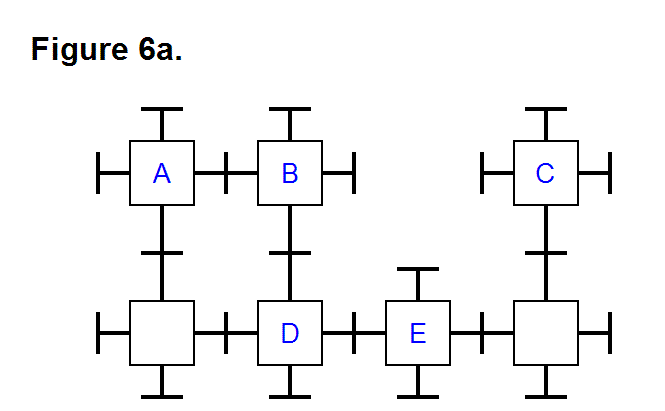
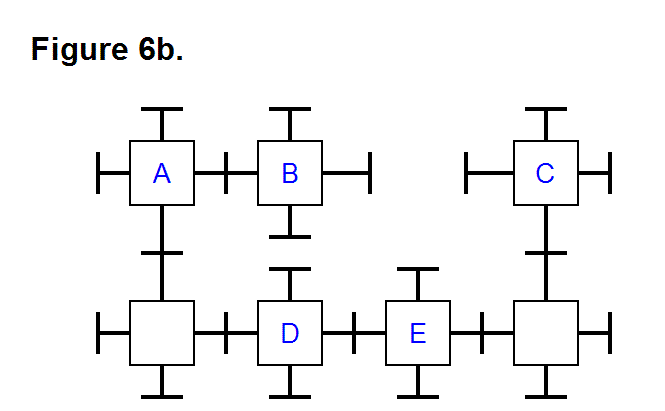
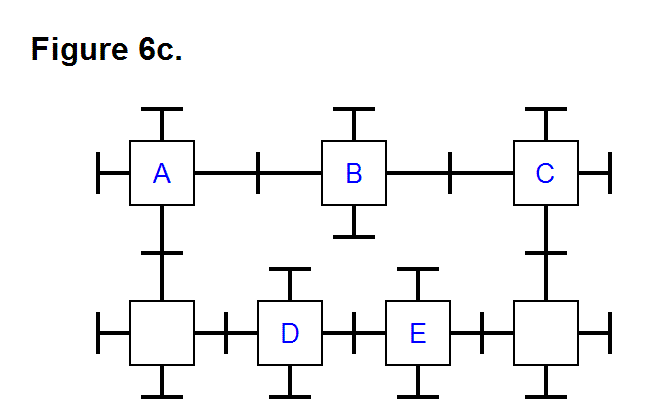
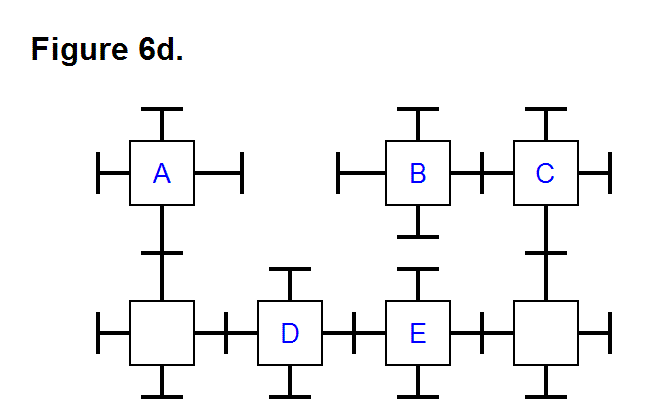
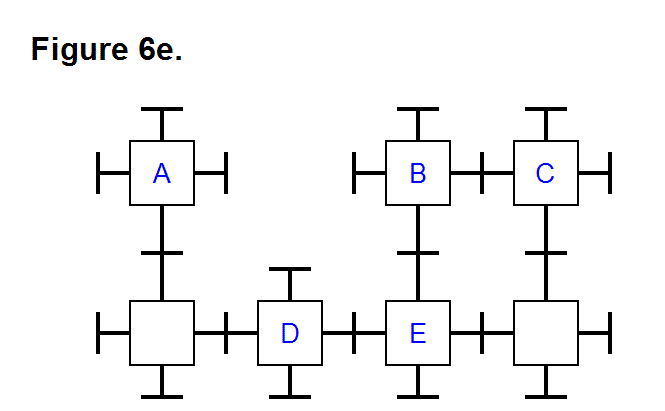
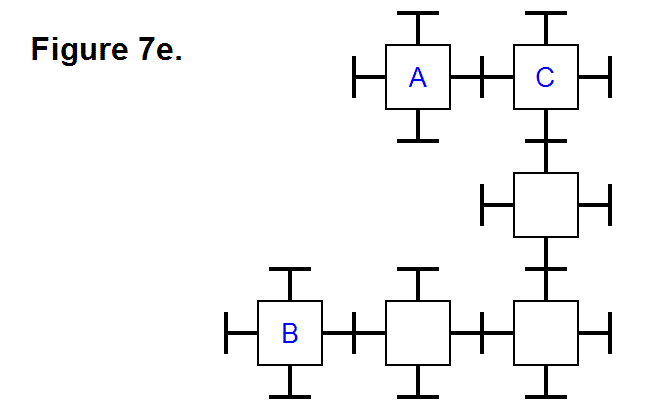
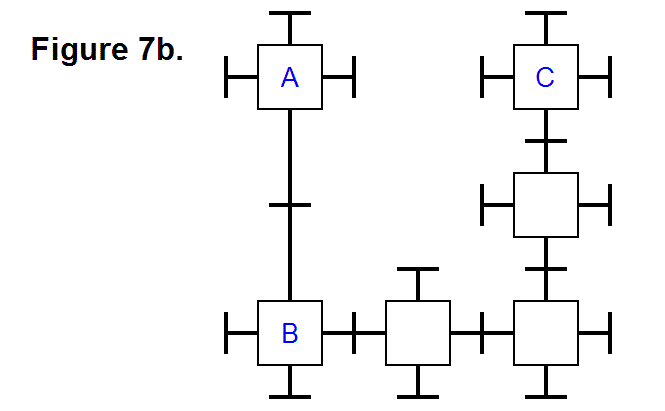
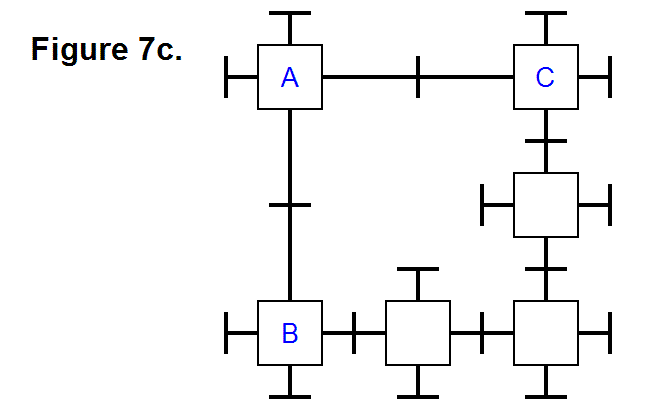
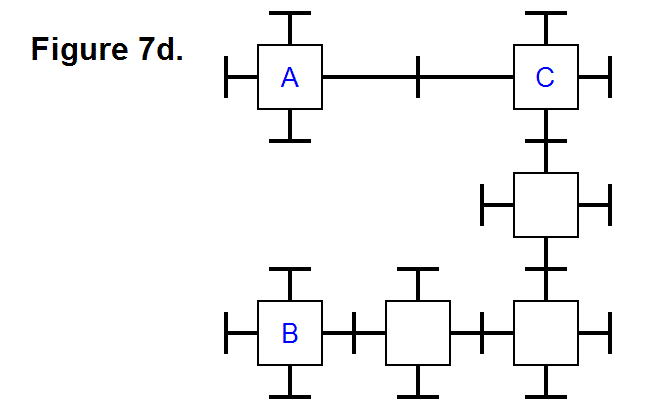
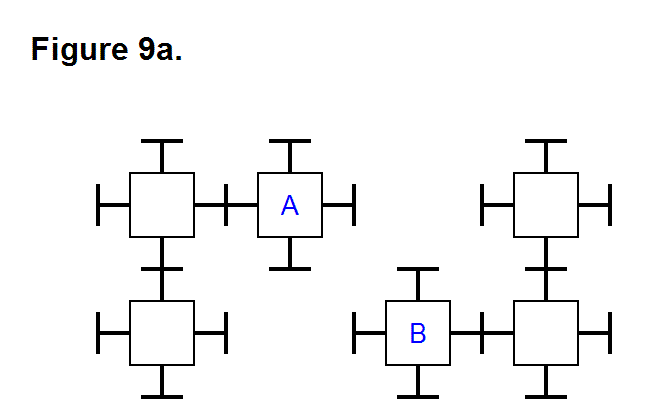
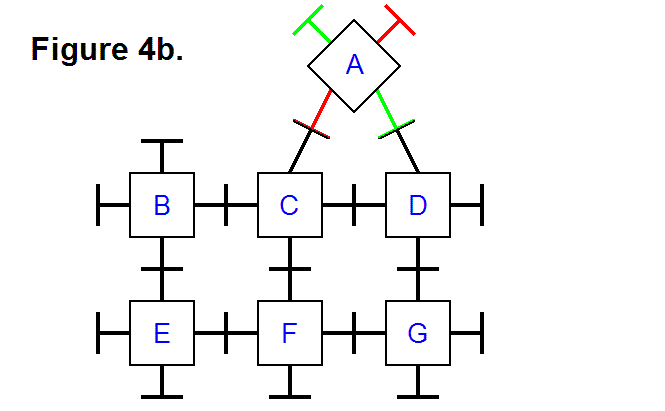
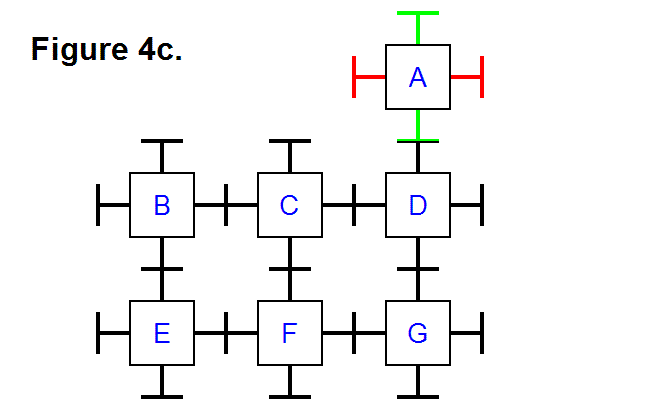
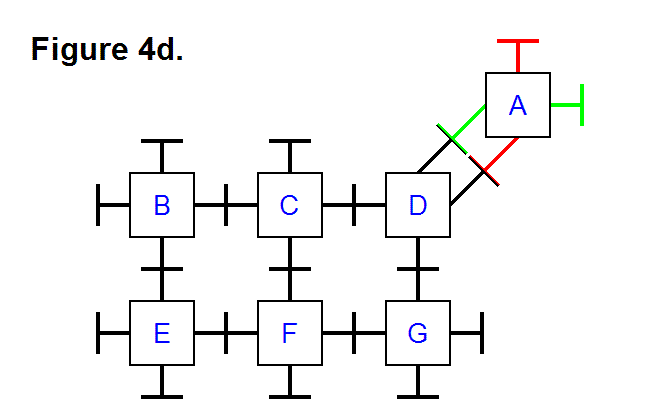
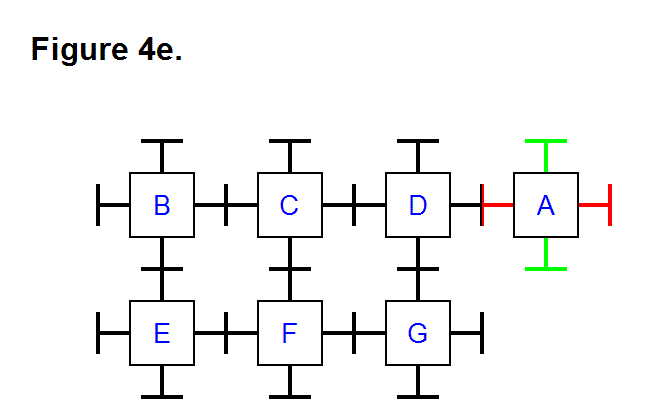
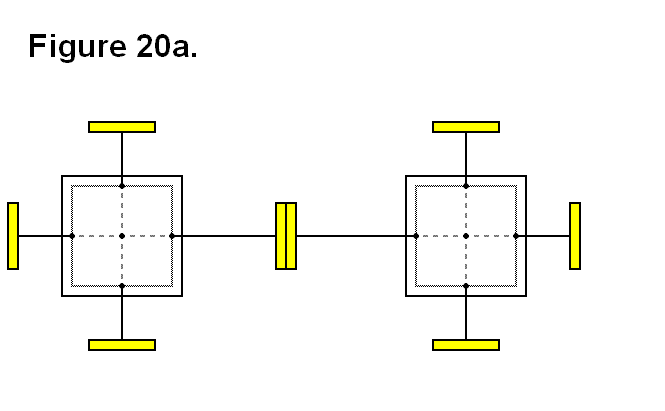
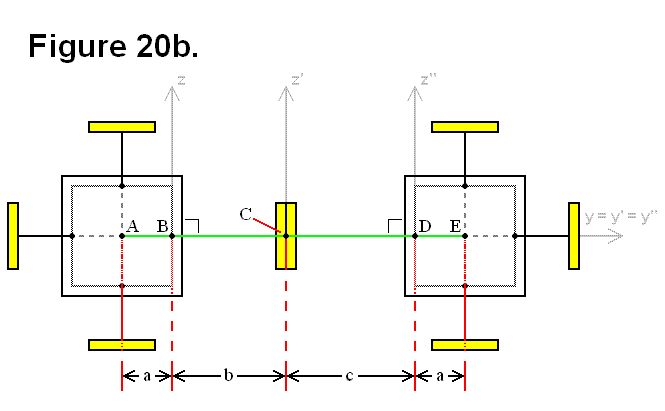
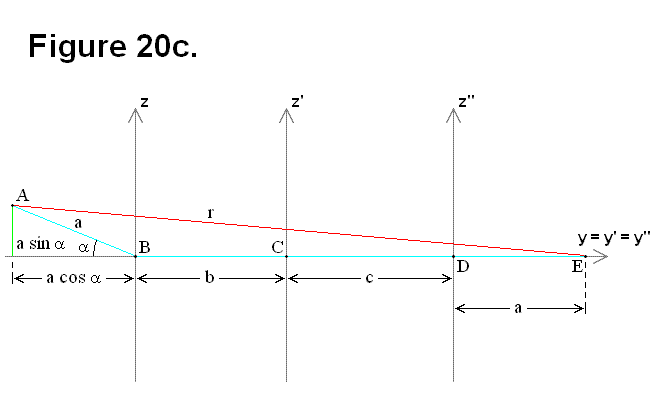
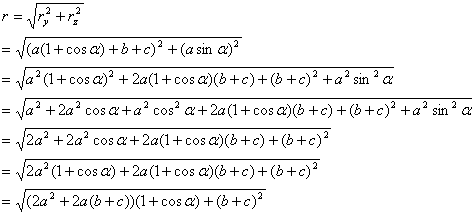Extending/Retracting Matrix Effect

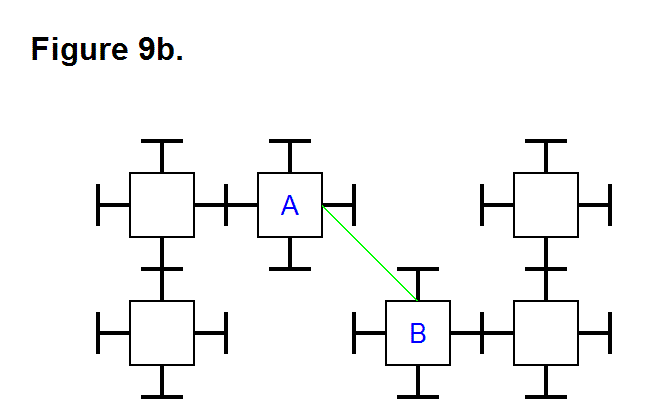
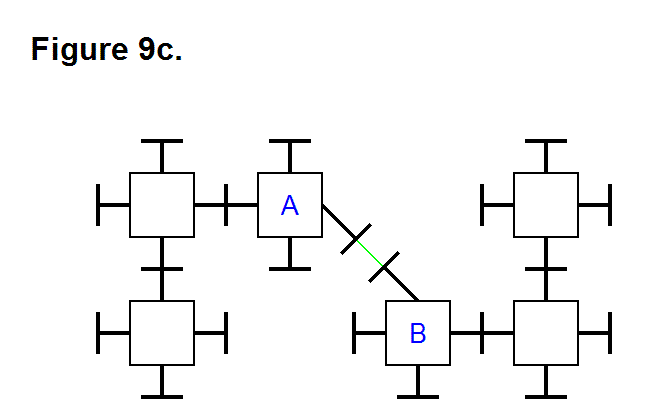
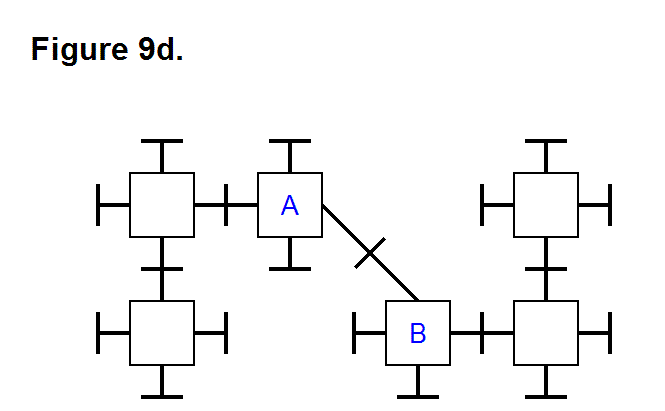
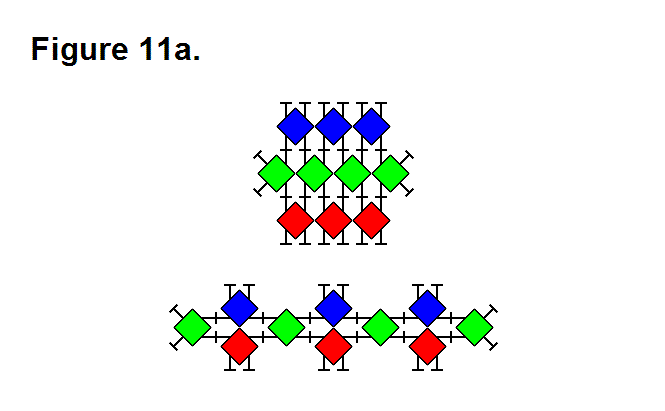
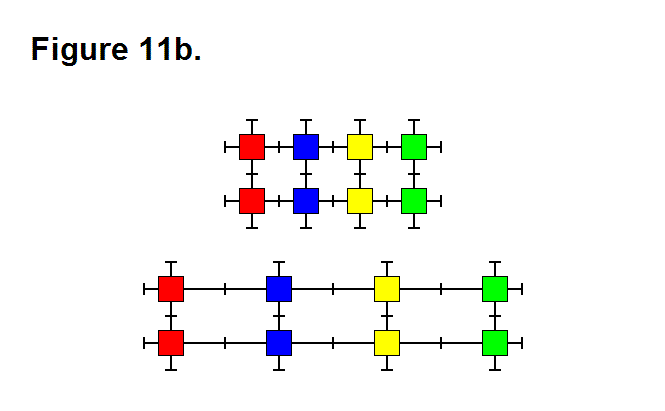
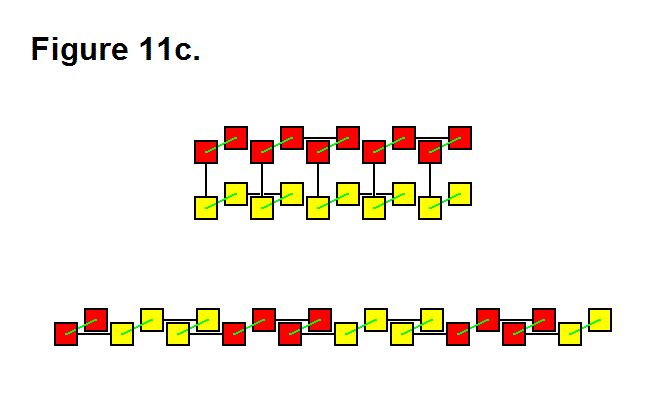
Posted on by HTDNET Support Services

EXTENDING/RETRACTING MATRIX EFFECT

There are 3 basic means that a matrix can use to produce an extending or retracting effect; these are pivoting the legs (Figure 11a, below), telescoping the legs (Figure 11b, below), or rotating the connecting plate surface (Figure 11c, below). They can be performed in any combination with each other, and using all of them can be used to maximize the ratio between highest and lowest matrix densities. In the figures below, the upper image shows the matrix retracted and the lower image shows the matrix extended. In Figure 11c, the legs with the connecting plates that rotate are shown in green between the module cores (red and yellow rectangles) in a 2-layer 3-dimensional representation; for the upper image, the red modules are in the upper rows and the yellow modules are in the lower rows.

 

     

 

Matrix Production of Rotational Motion

Posted on by HTDNET Support Services

MATRIX PRODUCTION OF ROTATIONAL MOTION

A matrix consisting of a large quantity of modules is capable of producing rotational motion. Figure 10a, shown below, shows a matrix in a ring configuration to produce this effect. It consists of an outer ring in red, and an inner ring in blue. It can be more than one ring layer of modules thick. The box shows an enlarged “under the microscope” view of the individual modules that make up a portion of the ring matrix. The center column, in green, consists of modules that repeatedly connect and disconnect to the red and blue columns of modules and forms a ring layer in the matrix between the red and blue rings. For the red ring to produce a clockwise rotation motion in the blue ring, the legs on the modules in the green column and on the modules in the columns on either side of the green column that connect to the green column pivot clockwise when not connected together and counter-clockwise when connected together. They do the reverse to produce a counter-clockwise rotational motion in the red ring.

The maximum rotational speed produced by this matrix structure is fairly slow; for example, suppose that it has a radius of 10 feet; it will hypothetically only be able to produce 1 cycle per minute of rotational motion (or 1 RPM). By connecting several matrices of rings together in series in a certain way the angular speed can be doubled for each additional layer. Figure 10b, shown below, shows a matrix in image (1) consisting of two cylinders in red and blue connected together by a truncated cone section in gray. This matrix structure by itself does not produce rotational motion; it is a rigid object. Image (2) shows how two matrix objects structured this way can combine to form another complex matrix structure that layers the blue section for the matrix on the right in the red section of the matrix on the left to produce rotational motion, which corresponds to the matrix in Figure 10a. The five matrices connected together in series in image (3) have 4 layers that can produce a relative rotational speed that is 8 times the rotational speed of a single layer of 2 matrices connected together between the matrix structures at the ends of this complex matrix structure. The calculation is 25-2 = 8, where the 5 is the number of matrix structures and the rest of the numbers are constants. If 1 layer is capable of producing a maximum of 1 rotation per minute, then 4 layers is capable of producing 8 rotations per minute and 12 layers is capable of producing somewhere in the vicinity of two thousand rotations per minute (hypothetically, 2,048 RPM).

In general, the hypothetical formula for the total maximum rotational speed output is

sn-1 = 2n-2∙s1

where sn-1 is the total maximum rotational speed, n is the number (greater than 1) of matrix structure objects such as the one in image (1) of Figure 10b, and s1 is the maximum rotational speed output of two of these matrix structure objects. This means a very large rotational speed can be produced by having many matrices that produce rotational motion in series, but this is limited by the tension produced by the centrifugal forces in the matrices that are rotating at faster speeds. Factors such as radius, density of the modules (mass), friction from wind resistance, and maximum tension that the modules can handle have to be taken into consideration to determine the actual upper limit of sn.

Making Accelerometers Using Modules in a Matrix

Posted on by HTDNET Support Services

MAKING ACCELEROMETERS USING MODULES IN A MATRIX

Although the modules can be produced so that each one has its own accelerometer, it is perhaps better that this option not be utilized, especially for matrices that would consist of large numbers of modules, for the following reasons:

  1. It is more expensive to mount an accelerometer element in each module.
  2. Generally it is unnecessary for a matrix to consist of modules that each contain an accelerometer.
  3. A matrix can build accelerometers that are located throughout the structure positioned where desired.

In Figure 15a, the matrix is a simple example of a structure with a pendulum, the blue modules, for an accelerometer. The red modules symbolize a simplified cross section of an implemented structure. When the structure is subjected to horizontal acceleration, the pendulum, which is connected to the rest of the structure by the green module, will pivot the leg of the green module to which it is connected and in neutral (i.e., it is not locked from moving). The green module’s leg, which is connected to the pendulum, uses the sensors for measuring the angle of the leg’s position to measure acceleration of the structure in the horizontal plane.

Figure 15b shows how a matrix can build a gravimeter. As the structure, which is shown simplified as the red shaded modules and in 2 of 3 dimensions, is subjected to forces, the block of blue modules affect the green modules that connect it to the rest of the structure. In a similar way that the leg of the green module is driven by the pendulum in Figure 15a to act as a sensor, the green modules in Figure 15b also use the pivoting and telescoping position sensors in their legs that are chained together to measure forces placed on the structure. An actual gravimeter would consist of having a 3rd row of green modules perpendicular to the plane of the image and connected to a 3-dimensional block of the blue shaded modules. The forces that it measures can be both translational as well as rotational. Since the effects of external forces are conservative, it is necessary for the green modules to implement feedback systems that poll for the actual presence of forces by measuring the resisting effect of actuating the leg. For example, when the external forces are removed, the green modules have to re-center the block of blue modules for “synthesizing” the effect of equilibrium.

In practice, a matrix implemented into a structure can randomly use almost any module “on-the-fly” as an accelerometer. This basically means that any matrix implemented into a structure practically has the inherent built-in feature of having accelerometers, even though there are no elements present in the modules designed to function as accelerometers.

Module Connection Arrangement Patterns of a Cell

Posted on by HTDNET Support Services

MODULE CONNECTION ARRANGEMENT PATTERNS OF A CELL

A cell can be composed of a varying number modules, sometimes in various combinations for a given number of modules. When there can be various combinations for a given number of modules, there can be some arrangements that are not appropriate. Figure 19a shows 3 Core Base Assemblies, the objects consisting geometrically of two rectangular boxes and a square truncated pyramid with sides that slope at 45° angles that are part of the modules, connected together in such a way that they share a common corner. One of these modules has a gray shaded truncated pyramid for future reference. In this case the arrangement of modules is appropriate.

Figure 19b also shows 3 Core Base Assemblies connected together in such a way that they share a common corner, but they are a mirror image pattern of the 3 Core Base Assemblies of Figure 19a. This is also an appropriate arrangement of modules. The Core Base Assemblies of Figures 19a and 19b are opposite halves of a cell that can be joined together to form a whole cell.

Figure 19c shows two modules connected together. This pattern is the only way any two modules can be joined together when there are only two; the bottom one can, for example, be assigned identification number 1 (ID #1) and the other would be assigned ID #2. There are four sides and two types of sides; the type of side is used as a reference to determine which has ID #1 or ID #2. If a third module is added to the pattern, using the Cube Face Numbering Convention article as a convention reference, then to Figure 19c the module with the gray pyramid in Figure 19b would be assigned ID #3; and in Figure 19a it would be assigned ID #4 since the first two modules are in reverse positions. Three of the arrangements of modules in Figure 19c can be joined together to form a whole cell.

Figure 19d shows the same two modules of Figure 19c in a 2-dimensional side view.

Figure 19e shows a third module added to the arrangement of modules from Figure 19d. This is not an appropriate arrangement of modules, and can be determined because there are more than two modules connected together and none of them share a common corner. One reason it is not appropriate is because if the pins-and-hole system that joins two modules together are not designed to latch the modules together (e.g., the pin is a simple cylinder), then this arrangement will not allow the modules to latch together to bond.

Figure 19f shows the arrangement of Figure 19e with a fourth module added to the back, shown partially out of view, in green, and with a gray pyramid. This arrangement of modules is appropriate, since each module shares a common corner with two of its adjacent modules. The arrangement of modules in Figure 19c can be joined to the arrangement of modules in Figure 19f to form a whole cell.

Figure 19g shows three modules arranged in the complementary arrangement of the ones in Figure 19e, and is also not an appropriate arrangement of modules for the same reason, and also because the two opposite modules won’t have the direct electronic connections described in the Pattern for Element Core Electronic Connections article. The two arrangements of modules in Figures 19e and 19g can join together to form a whole cell.

Figure 19h shows four modules in a ring pattern, and it is also not an appropriate arrangement of modules for the same reasons given for the three of Figure 19g.

Although a fourth module with a gray pyramid is added, shown partially out of view and in green and yellow, to the arrangement of Figure 19g to form the arrangement of Figure 19i, there is no difference in the pattern arrangements of Figures 19i and 19f other than the gray one being in a different position in the pattern.

Figure 19j shows five modules connected together, made by connecting a fifth module to the top of the pattern of modules shown in figure 19i. This is the only way five modules can be connected together to form part of a cell. 

In Summary, the following table shows the possible number of arrangements for a given number of modules in a cell:

number of modules in a cell 2 3 4 5 6
possible number of arrangements 1 4 2 1 1

There are only two number-of-modules-in-a-cell situations where there are multiple possible number-of-arrangements of modules, for 3 and 4 modules. For 3 modules, 2 are appropriate and 2 are inappropriate; for 4 modules, 1 is appropriate and 1 is inappropriate.

Connecting Plates Alignment Requirement

Posted on by HTDNET Support Services

CONNECTING PLATES ALIGNMENT REQUIREMENT

When the connecting plates of two different cells engage each other to connect to bond together correctly, the axis going though the center of each telescoping shaft and connecting plate have to be both parallel and aligned with each other; in other words, they both have to share a common axis. The reason this is necessary is to be able to utilize the entire area of the connecting plate of each module against moment forces, and large tension or compression forces along the telescoping shaft (module leg) axes. Figure 17a shows part of two telescoping shafts and side views of their connecting plates for two different modules; one of the connecting plates is blue and the other is red. The dashed green line through each telescoping shaft and connecting plate indicates the axis of the leg and connecting plate, and at the same time shows that they both share a common axis.

In figure 17b, the two legs and connecting plates of figure 17a are shown as parallel but not aligned to each other to share a common axis.

If the two connecting plates from figure 17b try to engage to bond together along their axes, they will come in contact as shown in figure 17c; since they aren’t aligned they won’t be able to bond, at least not properly if even possible at all. This type of contact is acceptable if it is not necessary for the two modules to bond together and if there isn’t going to be an excessive amount of force or pressure between them.

Figure 17d shows the two modules of figure 17a in contact for correctly connecting together; they might or might not be bonded together.

Lateral Lattice Reconfiguration Using Leg Extending Capabilities

Posted on by HTDNET Support Services

LATERAL LATTICE RECONFIGURATION USING LEG EXTENDING CAPABILITIES

This type of modular self-reconfigurable system is capable of lattice based transformations to change its shape by using the leg extending and retracting feature. Figure 6a shows several modules initially in a state where there is an empty space above module E and between modules B and C. The following example shows how the modules in this matrix can translate a module to fill in this empty space by moving another module to that location. 

Figure 6b shows the first transition state of the matrix given in Figure 6a. It involves disconnecting and shortening the legs between modules B and D, and beginning the process of extending the legs between modules B and C to join them together.

Figure 6c shows module B translating horizontally by extending the leg connections between modules A and B until the extending legs between modules B and C join together.

Figure 6d shows modules A and B disconnecting from each other and retracting, and the use of module C to align module B above module E by shortening the legs connecting modules B and C together.

Figure 6e shows the legs for modules B and E extending and joining together and the legs that disconnected between modules A and B completely retracted; this completes the transition.

This matrix could also have accomplished the same goal, also with lattice transitions, by first extending the legs between modules B and C to connect to each other, then disconnecting and shortening the legs that join modules B and D together, then shortening the legs that join B and C together, then finally extending the legs between modules B and E to connect these modules to each other. This version describes how it is possible to accomplish this task without the first column of modules in the matrix.

Diagonal Lattice Reconfiguration Using Leg Extending Capabilities

Posted on by HTDNET Support Services

DIAGONAL LATTICE RECONFIGURATION USING LEG EXTENDING CAPABILITIES

This type of modular self-reconfigurable system is capable of lattice based transformations to change its shape by using the leg extending and retracting feature. Figure 7a shows a matrix consisting of a column on the left with 2 modules which is connected to another module in the middle column on the bottom row, and it is connected to the bottom of a column of 3 modules on the right. The following example shows how the modules in this matrix can translate a module to move it both horizontally and vertically.

Figure 7b shows the first transition state of the matrix given in Figure 7a. It involves extending the legs between modules A and B to translate module A vertically.

Figure 7c shows modules A and C extending legs between them and joining them together.

Figure 7d shows modules A and B disconnecting from each other and retracting the legs between them.

Figure 7e shows the legs between modules A and C retracting to translate module A horizontally.

Module A has now been translated out of the first column into the second column and out of the second row into the first row, and this was accomplished using only lattice transitions. In a similar matrix arrangement, the same type of goal could have been accomplished by first extending the legs of the two middle row modules to join, then disconnecting the legs between modules A and B, then shortening the legs that join module A to the module in the column of modules on the right to translate module A to the second column, then connecting the leg from module A to the module in the middle column and bottom row, then disconnecting the legs that join module A to the module in the column on the right, then extending the legs that join module A to the module in the bottom row to translate module A to the top row, then connecting the legs between modules A and C, then finally disconnecting and retracting the legs between module A and the module in the bottom row.

Aligning Legs for Joining Connecting Plates

Posted on by HTDNET Support Services

ALIGNING LEGS FOR JOINING CONNECTING PLATES

To join together two modules that are not aligned, in positions where all that is necessary is to extend the appropriate legs, both of these legs have to pivot to the correct angle. Figure 9a, shown below, is an example of two modules A and B that are not connected directly to each other in a matrix.

Suppose the right leg of module A and top leg of module B are selected for connecting these modules together. Figure 9b, shown below, shows the common axis along which these legs must align for connection as a green line.

Figure 9c, shown below, shows the legs for modules A and B in new positions after they have pivoted to the angle to align them to their common axis, shown as a green line, for joining together.

These legs are now aligned so that all that is is necessary for modules A and D to join together is to extend the legs. Figure 9d, shown below, shows modules A and B joined together after the legs have been extended.

If modules A and B are in the same matrix system and approximal, then it is not necessary to use any sensors or external input data to determine that the legs are aligned for joining. If modules A and B are in different matrix systems or a significant enough distance apart to be able to geometrically introduce an alignment discrepancy in the same matrix system, then it is necessary to use sensors or external input data to determine that the legs are aligned for joining; this can be accomplished by placing several sensors on the surface of the connecting plate and a significant distance from the axis of the leg and connecting plate, near the perimeter of the connecting plate circle. Once they are in close enough proximity to detect the presence of each other by emitting signature signals, the differences in strength of the signals determines whether or not the legs need to pivot until the signal strengths are equal to each other. This is usually a basic “reflex” action; an exception would be when the legs reach their pivoting limit. This pivoting limit is a minimum of 45° in any direction from the center axis perpendicular to the face of the module core assembly, or core “cube,” and will probably not be more than a few degrees beyond this because of the limitations imposed by the design of the module’s mechanical structures. In a situation where the legs cannot pivot to align to their common axis, the modules can still join together by carrying out more complex movements involving having the matrices change the positions of these modules and other modules that are adjacent to them in such a way that they can join together.

 

Basic Module Transfers, Movements, and Connections

Posted on by HTDNET Support Services

BASIC MODULE TRANSFERS, MOVEMENTS, AND CONNECTIONS

A module can be transferred around in a matrix of modules by pivoting and telescoping the legs, and connecting and disconnecting with the connecting plates. In Figure 4a, below, modules A-E are connected together to form a two dimensional matrix; in this matrix, module A is initially positioned in row 1, column 2, and its bottom leg connects to the top leg of module C, positioned in row 2, column 2. Module C is connected to and supported by the rest of the modules in the matrix through its bottom, left, and right legs. In the following figures, the legs for module A are drawn in different colors to illustrate their location in the movement as the module progresses from one position to another.

It is possible to transfer module A from row 1, column 2 to row 1, column 3, along the top surface of the rest of the matrix. Figure 4b, below, shows the same modules in Figure 4a, except that module A has been tilted by pivoting its bottom leg and the top leg of module C. The leg to the right of module A and the top leg of module D have also pivoted so the plates on the legs of these modules can connect to each other. The legs that pivot can also be extended so the connecting modules can reach each other, if necessary.

By reversing the motion of moving module A with module C and connecting it to module D, that is, disconnecting module A from module C and pivoting it upright with module D, module A is now in row 1, column 3; this is shown in Figure 4c, below.

It is also possible to pivot a module around a corner of the matrix, such as with module A around module D from its top to its right side (position row 1, column 3 to position row 2, column 4). Figure 4d, below, shows the legs that connect modules A and D (the top leg of module D and the bottom leg of module A from Figure 4c) pivoted to allow the right leg of module D to pivot and connect to the bottom leg of module A (the same leg that was on the right side of module A in Figure 4c.), which was also pivoted into position for connecting to the leg from module D.

Finally, just as reversing the movement pattern halfway through the process of transferring module A from position row 1, column 2 to position row 1, column 3 could be used to accomplish that process in Figures 4a, 4b, and 4c, the same concept can also be applied to transferring module A from position row 1, column 3 to position row 2, column 4. Figure 4e shows the final result with module A in position row 2, column 4.

At this point it’s trivial to determine that module A can travel all the way around the rest of the matrix of modules B, C, D, E, F, and G, back to its initial position, by repeatedly applying the basic techniques of transferring a module along a row from one column to another, as well as around corners. Transferring a module vertically from one row to another in the same column involves using the same technique as transferring a module from one column to another column in the same row. In general, any module can be positioned to any other location to reshape either a 2-dimensional or 3-dimensional matrix consisting of any number of modules into any combination of connected patterns. Figure 4b shows how the modules in a matrix are not limited to being connected in a rectangular cycle arrangment (e.g., the way modules B, C, E, and F form a cycle); they can also be connected in a triangular cycle arrangement (e.g., the way modules A, C, and D form a cycle). Notice, also, that in Figure 4d modules A and D are connected together with two pairs of legs each; by using this feature it is possible to connect a series of several modules in this way, to double the tension strength. In a 3-dimensional matrix of modules, up to three pairs of legs can be connected between modules to triple the tension strength in a series of modules that are connected together in this way, since there are 6 legs for each module (instead of just 4 legs for each module as in a 2-dimensional matrix).

Determining the Distance Between the Centers of Two Cells Connected Together

Posted on by HTDNET Support Services

DETERMINING THE DISTANCE BETWEEN THE CENTERS OF TWO CELLS CONNECTED TOGETHER

The geometric structural topology of a full cell consists of it having the following fundamental characteristics:

  1. the distance between the center of a cell and the point at which each leg pivots is a constant value
  2. for each cube face, the distances between the center of a cell and the point at which each leg pivots are all equal to each other
  3. for each cube face, the line segment between the center of a cell and the point at which each leg pivots is perpendicular to the line segments corresponding to each of the four adjacent cube faces

Many other characteristics about the topology of a cell can be derived from these fundamental characteristics and geometry. An essential key for a mesh of cells to form into objects is knowing its fundamental geometric structural topology and the distance between the centers of two cells connected together; this can be derived given that the following information is known about the modules in each cell that connect the two cells together:

  1. the length of the telescoping leg (this value is a variable within a fixed range)
  2. the angle a leg is pivoted, given as a value from a position perpendicular to the face of the cube; the absolute value of the angle a leg is pivoted will not be more than somewhere in the vicinity of 60 degrees
  3. either the actual connecting plate relative angle of rotation or the virtual connecting plate relative angle of rotation (i.e., derived from the effect of pivoting a leg about both of its cube face-oriented pivoting axes)

Figure 20a shows two cells connected together using a similar illustration convention as shown in Figure 12a from the article Geometrical Cell Dimension Limits and Requirements.

Figure 20b shows the same two cells connected together from Figure 20a including some 2-dimensional cartesian axes, labels for certain points, and labels for distance between these points. For the cartesian axes, the y, y’, and y” (from here on a dimension shall be generalized in the form w(n)) axes are all parallel and aligned along the y-dimension origin; the x(n) (for a 3rd dimension, shown in Figure 20e) and z(n) axes are all parallel to their corresponding dimensions. The legs that connect two cells together are always parallel and aligned about their axes; in Figure 20b they are aligned parallel to the y(n) axes and with the z(n) axes origins. The z’-axis is aligned to be centered at point C. The z-axis and z”-axis are arranged to be placed in alignment with the leg pivoting points B and D, respectively. In this case, both legs have pivot angle values of 0. Points A and E are the centers of their corresponding cells. Points B and D are the points at which each corresponding leg pivots. Point C is the center of the two connecting plates that are connected together. The distance between points A and B is the constant value a, which is equal to the distance between points D and E; this value corresponds to the distance described by the first list shown above, the fundamental geometric structural topology characteristics. The length of the telescoping leg from the left cell is b, which is the distance between the points B and C. The length of the telescoping leg from the right cell is c, which is the distance between the points Cand D. These leg lengths correspond to the first piece of information from the second list shown above.

In this case, determining the distance r between the centers of each cell is straighforward:

  (Formula #1)

In Figure 20c, the labelled points and corresponding distance labels of Figure 20b are shown without the cell body diagram illustrations and with one of the legs pivoted an angular value of α.

In this case the distance r between the centers of each cell is computed using the following equations and formula:

  (Formula #1a)
  (Formula #1b)
  (Formula #2)

In Figure 20d, both legs are pivoted about parallel normal vectors, meaning all the labelled points (A, B, C, D, and E) lie on the same plane, thus only a 2-dimensional diagram is necessary for analysis; the second leg is pivoted with an angular value of β.

For this situation, calculating the distance r between the centers of each cell needs to be computed using the following equations and formula (Equation # 2b was plugged in) by either changing the definition of the angles to take a polar coordinate format about their corresponding origins, instead of being an absolute value format, or switching from plugging in Equation # 2b to plugging in Equation # 2c into Formula # 3 when the centers of the cells are on opposite sides of the z(n) axes from each other.

  (Formula #2a)
  (Formula #2b)
  (Formula #2c)
  (Formula #3)

In Figure 20e, not only are both legs pivoted about the y(n) axes, but also not all the labelled points (A, B, C, D, and E) have to lie on the same plane, thus a 3-dimensional diagram is necessary for analysis. The difference between Figure 20d and Figure 20e can be interpreted as a result of at least one of two reason:

  1. Connecting plate rotation took place between the two connecting plates connecting the cells together (at point C).
  2. Pivoting of one of the legs connecting the two cells together about the x(n)-y(n) plane took place.

The actual connecting plate relative angle of rotation or the virtual connecting plate relative angle of rotation (i.e., produced as a result of pivoting the legs) is the angular value f.

The following equations and formula are used to calculate the distance r between the centers of each cell for the case of Figure 20e. In this format the x(n)-component of the point A (the center of the cell on the left) is held fixed equal to 0. If necessary, as an intermediate step the modules can use the equations to derive calculated values and then re-apply those values to the formula using the same equations for calculating the distance r; this occurs when the pivot of the leg for the cell on the left is actually the resultant of the leg pivoting on both axes, when none of the legs on the faces adjacent to the legs connecting the cells together lie on the same plane, or when there is both leg pivoting and plate rotation. This principle is true for the apparent discrete cases of Figure 20d where all the labelled points (A, B, C, D, and E) happen to lie on the same plane; all that is necessary for this situation is to utilize the 3-dimensional approach for Figure 20e. It is not necessary to be concerned about whether or not the centers of the cells are on opposite sides of the z(n) axes from each other, as it was for the case of Figure 20d, because this is resolved by having equations for all 3 dimensions.

  (Formula #3a)
  (Formula #3b)
  (Formula #3c)
  (Formula #4)

In general, only Formula # 4 is needed to calculate r for all cases. By knowing the geometric structural topology of the cells, and for every cell the angle values α, β, f, the values for lengths a, b, c, and the distance between the centers of any two two cells r, a mesh of cells has all the information about cell positions and states that it needs for knowing the state of its structure, and it has the geometric information that is necessary for changing its shape.